foreststill.blogg.se - Parallelogram picture shapes

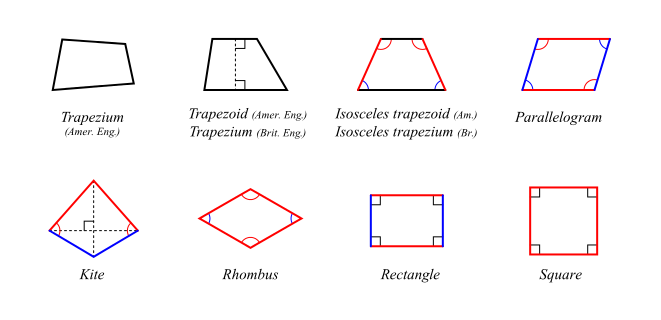
If it has four lines of reflectional symmetry, it is a square. If it also has exactly two lines of reflectional symmetry then it must be a rhombus or an oblong (a non-square rectangle). A parallelogram has rotational symmetry of order 2 (through 180°) (or order 4 if a square).Any non-degenerate affine transformation takes a parallelogram to another parallelogram.Any line through the midpoint of a parallelogram bisects the area.The area of a parallelogram is also equal to the magnitude of the vector cross product of two adjacent sides.The area of a parallelogram is twice the area of a triangle created by one of its diagonals.Opposite sides of a parallelogram are parallel (by definition) and so will never intersect.Thus all parallelograms have all the properties listed above, and conversely, if just one of these statements is true in a simple quadrilateral, then it is a parallelogram. There is a point X in the plane of the quadrilateral with the property that every straight line through X divides the quadrilateral into two regions of equal area.(This is an extension of Viviani's theorem.) The sum of the distances from any interior point to the sides is independent of the location of the point.The sum of the squares of the sides equals the sum of the squares of the diagonals.Each diagonal divides the quadrilateral into two congruent triangles.One pair of opposite sides is parallel and equal in length.Two pairs of opposite angles are equal in measure.Two pairs of opposite sides are equal in length.Two pairs of opposite sides are parallel (by definition).Square – A parallelogram with four sides of equal length and angles of equal size (right angles).Ī simple (non-self-intersecting) quadrilateral is a parallelogram if and only if any one of the following statements is true:.Any parallelogram that is neither a rectangle nor a rhombus was traditionally called a rhomboid but this term is not used in modern mathematics. Rhombus – A parallelogram with four sides of equal length.

Rectangle – A parallelogram with four angles of equal size (right angles).

7.3 Tangent parallelogram of an ellipse.

7 Parallelograms arising from other figures.

5 Proof that diagonals bisect each other.

4.1 Area in terms of Cartesian coordinates of vertices.

The etymology (in Greek παραλληλ-όγραμμον, parallēl-ógrammon, a shape "of parallel lines") reflects the definition. The three-dimensional counterpart of a parallelogram is a parallelepiped. The congruence of opposite sides and opposite angles is a direct consequence of the Euclidean parallel postulate and neither condition can be proven without appealing to the Euclidean parallel postulate or one of its equivalent formulations.īy comparison, a quadrilateral with just one pair of parallel sides is a trapezoid in American English or a trapezium in British English. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure. In Euclidean geometry, a parallelogram is a simple (non- self-intersecting) quadrilateral with two pairs of parallel sides. This parallelogram is a rhomboid as it has no right angles and unequal sides.Īb sin θ (product of adjacent sides and sine of the vertex angle determined by them)